Left To Face / NOVÉ EP !

Limita funkce více proměnných

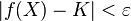O funkci $f (x i)$ n-proměnných $x i$ říkáme, že má v bodě $A = [a 1, a 2,..., a n]$ limitu K, pokud ke každému (libovolně malému) číslu $\varepsilon>0$ existuje takové číslo $δ > 0$ , jenž je v obecném případě závislé na volbě $\varepsilon$ , že pro všechny body $X = [x 1, x 2,..., x n]$ z $δ$ -okolí bodu A s výjimkou samotného bodu A platí $|f(X)-K|<\varepsilon$ . Takovou limitu značíme některým z následujících způsobů.

$\lim_{X \to A} f(X)=K$
$\lim_{[x_1,x_2,...,x_n] \to A} f(X)=K$
$\lim_{[x_1,x_2,...,x_n] \to [a_1,a_2,...,a_n]} f(X)=K$
$\lim_{\begin{matrix} x_1 \to a_1 \\ x_2 \to a_2 \\ \vdots \\ x_n \to a_n \end{matrix} } f(X)=K$

Limita funkce n proměnných je tedy definována obdobným způsobem jako limita funkce jedné proměnné.

U funkce n proměnných je možné provádět limitní přechod nejen vůči všem proměnným, tzn. $\lim_{X \to A}$ , ale také vzhledem několika nebo jen jedné z proměnných, tzn. např. $\lim_{x_3 \to a_3}$ . Tedy např.

$\lim_{x_1 \to a_1} f(x_1,x_2,...,x_n) = g(x_2,x_3,...,x_n)$ ,

kde g je funkcí $n - 1$ proměnných.

[editovat] Limita komplexní funkce

O komplexní funkci $f (z)$ definované v okolí bodu $z 0$ říkáme, že má v $z 0$ limitu $A$ , jestliže k libovolnému $\varepsilon > 0$ existuje $δ$ -okolí bodu $z 0$ takové, že

$| f(z) - A | < \varepsilon$

Limitu v bodě $z 0$ zapisujeme

$\lim_{z \rightarrow z_0} f(z) = A$ .

Formálně je tedy zápis stejný jako v případě reálných funkcí.

Limita $A$ může být komplexním číslem.

[editovat] Limita zprava a zleva

O funkci $f (x)$ říkáme, že má v bodě $a$ limitu $A$ zprava, resp. zleva, pokud k libovolnému číslu $\varepsilon>0$ existuje takové číslo $δ > 0$ , jehož hodnota může v obecném případě záviset na volbě $\varepsilon$ , že pro všechna x z pravého, resp. levého okolí bodu $a$ , z něhož vyjmeme bod $a$ , tedy pro všechna x splňující podmínku $0 < | x - a | < δ$ , platí $|f(x)-A|<\varepsilon$ , což zapisujeme

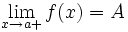$\lim_{x \to a+} f(x)=A \;$ - označována jako limita zprava 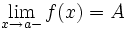$\lim_{x \to a-} f(x)=A \;$ - označována jako limita zleva

Funkce $f (x)$ má v bodě a limitu pouze tehdy, pokud má v tomto bodě současně limitu zleva i zprava.

Left To Face / NOVÉ EP ! pop / Třeboň

Kontakty

Novinky

limita posloupnosti-at vidite, proc jsme ukoncili nasi karieru..

Limita funkce více proměnných

[editovat] Limita komplexní funkce

[editovat] Limita zprava a zleva

Nově přidané fotky

Poslední názory

WayFu(c)k

WayFu(c)k

#zlatovlaska

#zlatovlaska

Stendee

Stendee

Podobné kapely

Suffer

Inside Pain

Exni!to

Kick 69

Vees